AUTOMATIC QUADRATURE SCHEME FOR CAUCHY TYPE SINGULAR INTEGRAL ON THE VARIABLE INTERVAL
DOI:
https://doi.org/10.46754/jmsi.2022.06.004Keywords:
Automatic quadrature scheme, Cauchy type singular integrals, Chebyshev Polynomials, Error estimationAbstract
In this note, we consider the product indefinite integral of the form
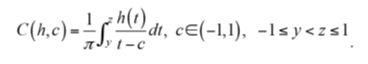
An automatic quadrature scheme (AQS) is constructed for evaluating Cauchy principal singular integrals in two cases. In the first case c∈ [y,z] ⊂ [-1,1] where -1 < y < z < 1, density function h(t) is approximated by the truncated sum of Chebyshev polynomials of the first kind. Direct substitution does not give solutions so we have used the AQS and reduced problems into algebraic equation with unknown parameters bk which can be found in terms of the singular point with some front conditions. In the second case c ∈ [-1,1], the application of the AQS reduced the number of calculations twice and accuracy is increased. As a theoretical result, the convergence theorem of the proposed method is proven in a Hilbert space. Numerical examples with exact solutions and comparisons with other methods are also given, and they are in the line with theoretical findings.
References
Stewart, C. E. (1960). On the numerical evaluation of singular integrals of Cauchy type. J. Soc. Ind. Appl. Math, 8(2), 342-353. DOI: https://doi.org/10.1137/0108021
D. F. Paget & D. Elliott. (1972). An algorithm for the numerical evaluation of certain Cauchy principal value integrals. Numerische Mathematik, 19, 373-385. DOI: https://doi.org/10.1007/BF01404920
M. M. Chawla & T. R. Ramakrishnan. (1974). Modified gauss-jacobi quadrature formulas for the numerical evaluation of cauchy type singular integrals. BIT, 14(1), 14-21. DOI: https://doi.org/10.1007/BF01933113
Ioakimidis, N. I., & Theocaris, P. S. (1977). On the numerical evaluation of cauchy principal value integrals. Rev. Roumaine Sci. Tech. S´er. M´ec. Appl, 22, 803-818.
G. Monegato. (1984). Convergence of product formulas for the numerical evaluation of certain two-dimensional cauchy principal value integrals. Numerische Mathematik, 43, 161-173. DOI: https://doi.org/10.1007/BF01390121
T. Hasegawa & T. Torii. (1991). An automatic quadrature for Cauchy principal value integrals. Mathematics of Computation, 56(194), 741-754. DOI: https://doi.org/10.1090/S0025-5718-1991-1068816-1
T. Hasegawa & T. Torii. (1987). Indefinite integration of oscillatory functions by the Chebyshev series expansion: Journal of Computational and Applied Mathematics, 17, 21-29. DOI: https://doi.org/10.1016/0377-0427(87)90035-5
T. Hasegawa, T. Torii, & H. Suguira. (1990). An algorithm based on the FFT for the generalized Chebyshev interpolation. Mathematics of Computation, 54(189), 195-210. DOI: https://doi.org/10.1090/S0025-5718-1990-0990599-0
Boykov, I. V. (2001). Numerical methods of computation of singular and hypersingular integrals. International Journal of Mathematics and Mathematical Sciences, 28(3), 127-79. DOI: https://doi.org/10.1155/S0161171201010924
T. Hasegawa & H. Suguira. (2007). Quadrature rule for indefinite integral of algebraic-logarithmic singular integrands. Journal of Computational and Applied Mathematics, 205(1), 487-496. DOI: https://doi.org/10.1016/j.cam.2006.05.025
Z. K. Eskhuvatov, N. M. A Nik Long & M. Abdulkawi. (2009). Quadrature formula for approximating the singular integral of Cauchy type with unbounded weight function on the edges. Journal of Computational and Applied Mathematics, 233, 334-345. DOI: https://doi.org/10.1016/j.cam.2009.07.034
Z. K. Eskhuvatov, A. Ahmedov, N. M. A. Nik Long & N. J. Amalina. (2011). Approximating cauchy type singular integral by an automatic quadrature scheme. Journal of Computational and Applied Mathematics, 235(16), 4675-4686. DOI: https://doi.org/10.1016/j.cam.2010.08.001
Kh. M. Shadimetov, A. R. Hayotov, & D. M. Akhmedov. (2015). Optimal quadrature formulas for Cauchy type singular integrals in Sobolev space. Applied Mathematics and Computation, 263, 302-314. DOI: https://doi.org/10.1016/j.amc.2015.04.066
T. T. Nhan. (2017). Simple method for evaluating singular integrals. American Journal of Computational Mathematics, 7(4), 444-450. DOI: https://doi.org/10.4236/ajcm.2017.74032
D. M. Akhmedov, A. R. Hayotov & Kh.M. Shadimetov. (2018). Optimal quadrature formulas with derivatives for cauchy type singular integrals. Applied Mathematics and Computation, 317, 150-159. DOI: https://doi.org/10.1016/j.amc.2017.09.009
H. R. Kutt. (1975). On the numerical evaluation of finite-part integrals involving an algebraic singularity (CSIR Special Rept. WISK 179). National Research Institute for Mathematical Sciences, Pretoria.
N. I. Ioakimidis. (1983). On the numerical evaluation of a class of finite-part integrals. ZAMM, 63, 572- 574. DOI: https://doi.org/10.1002/zamm.19830631108
P. A. Martin. (1992). Exact solution of a simple hypersingular integral equation. Journal Integral Equations Applications, 4(2), 197-204. DOI: https://doi.org/10.1216/jiea/1181075681
G. Monegato. (1994). Numerical evaluation of hypersingular integrals. Journal of Computational and Applied Mathematics, 50(1-3), 9-31. DOI: https://doi.org/10.1016/0377-0427(94)90287-9
P. A. Martin & F. J. Rizzo. (1996). Hypersingular integrals: how smooth must the density be? International Journal for Numerical Methods in Engineering, 39, 687-704. DOI: https://doi.org/10.1002/(SICI)1097-0207(19960229)39:4<687::AID-NME876>3.0.CO;2-S
C. Y. Hui & D. Shia. (1999). Evaluation of hypersingular integrals using Gaussian Quadrature. International Journal for Numerical Methods in Engineering, 44(2), 205-214. DOI: https://doi.org/10.1002/(SICI)1097-0207(19990120)44:2<205::AID-NME499>3.0.CO;2-8
I. V. Boykov, E. S. Ventsel & A. I. Boykova. (2009). Accuracy optimal methods for evaluating hypersingular integrals. Applied Numerical Mathematics, 59(6), 1366-1385. DOI: https://doi.org/10.1016/j.apnum.2008.08.004
Bichi S. L., Eshkuvatov Z. K., & Nik Long N. M. A. (2014). An automatic quadrature schemes and error estimates for semibounded weighted hadamard type hypersingular integrals. Abstract and Applied Analysis, 2014, 1-13, Article ID 387246. DOI: https://doi.org/10.1155/2014/387246
S. J. Obaiys, Z. K. Eshkuvatov, & N. M. A. Nik Long. (2013). On error estimation of automatic quadrature scheme for the evaluation of Hadamard integral of second order singularity. UPB Scientific Bulletin. Series A: Applied Mathematics and Physics, 75(1), 85-98.
Obaiys, S. J., Ibrahim, R. W., & Ahmad, A. F. (2019). Hypersingular integrals in integral equations and inequalities: Fundamental review study. In Dorin Andrica & Themistocles M. Rassias (ed.), Differential and Integral Inequalities (pp. 687-717). Springer. DOI: https://doi.org/10.1007/978-3-030-27407-8_25
Chai H., Bao Y., & Zhang Zh. (2021). Numerical solutions of hypersingular integral equations for interface circular crack under axisymmetric loadings author links open overlay panel. Engineering Analysis with Boundary Elements, 122, 35-42. DOI: https://doi.org/10.1016/j.enganabound.2020.09.016
Akhmedov, D. M., & Shadimetov, Kh. M. (2021). Optimal quadrature formulas with derivative for Hadamard type singular integrals. AIP Conference Proceedings, 2365(1), 020020. DOI:10.1063/5.0057124. DOI: https://doi.org/10.1063/5.0057124
J. C. Mason & D. C. Handscomb. (2003). Chebyshev polynomials. CRC Press LLC. DOI: https://doi.org/10.1201/9781420036114
S. L. Sobolev. (1988). Some applications of functional analysis to Mathematical Physics. Moscow: Nauka, (in Russian)
N. R. F. Elfakhakhre, N. M. A. Nik Long & Z. K. Eshkuvatov. (2017). Stress intensity factor for multiple cracks in half plane elasticity. AIP Conference Proceedings, 1795, Article number 020010, 2nd International Conference and Workshop on Mathematical Analysis 2016. DOI: https://doi.org/10.1063/1.4972154
Downloads
Published
Issue
Section
License
Copyright (c) 2022 PENERBIT UMT

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.


